Analysis of Chutes and Ladders

Introduction

A friend of mine has been playing the board game Chutes and Ladders recently with his son.  The game is pretty simple: starting off of the board (effectively on “square zero”), each player in turn rolls a die (actually, spins a spinner) and– if possible– moves forward the indicated number of squares in serpentine fashion on the board shown below:

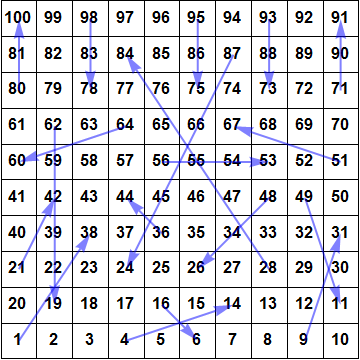
Chutes and Ladders board layout. In some variants, the chute from square 48 to 26 starts at square 47 instead.

If a player lands on the tail of an arrow, he continues along the arrow to the indicated square, ending his turn there.  (“Chutes” are arrows leading backward, and “ladders” are arrows leading forward.)  The first player to land exactly on square 100 wins the game.

My friend emailed me with the question, “What is the expected number of turns before the game is over?”  I think this is a nice problem for students, since it yields to the usual two-pronged attack of (1) computer simulation and (2) “cocktail napkin” derivation of an exact solution.

This is certainly not a new problem.  See the references at the end of this post for just a few past analyses of the game as a Markov chain.  My goal here is to provide an intuitive derivation of the exact expected length of the game as a solution to a system of linear equations, while staying away from the more sophisticated machinery of Markov chains, fundamental matrices, etc., that younger students may not be familiar with.

Unbounded vs. infinite

Before getting to the exact solution, though, it is worth addressing a comment in the referenced DataGenetics blog post about Monte Carlo simulation of the game:

“Whilst the chances of a game running and running are essentially negligible (constantly landing on snakes [i.e., chutes] and going around in circles), there is a theoretical chance that the main game loop could be executing forever. This is bad, and will lock-up your code. Any smart developer implementing an algorithm like this would program a counter that is incremented on each dice roll. This counter would be checked, and if it exceeds a defined threshold, the loop should be exited.”

I strongly disagree with this.  The valid concern is that there is no fixed bound on how many turns a particular simulated game might take; that is, for any chosen positive integer , there is a positive probability that the game will require at least turns, due to repeatedly falling backward down chutes.  However, the probability is zero that the game will execute forever; we can be certain that the game will always eventually terminate.  There is a difference between unbounded and infinite execution time.  In fact, such explicit “safety clamping” of the allowed number of moves implicitly changes the answer, modifying the resulting probability distribution (and thus the expected value) of the number of moves, albeit by an admittedly small amount.

There are situations where games can take an infinitely long time to finish– Chutes and Ladders just isn’t one of them.  For example, in this multi-round card game, everything is fine as long as .  And even when , the game is still guaranteed to finish, although the expected number of rounds is infinite.  But when , there is a positive probability that the game never finishes, and indeed continues “forever.”

Recursive expected values

To see how to analyze Chutes and Ladders, first consider the following simpler problem: how many times should you expect to flip a fair coin until it first comes up heads?  Let be this desired expected value.  Then considering the two possible outcomes of the first flip, either:

• It comes up heads, in which case we are done after a single flip; or
• It comes up tails… in which case we are right back where we started, and so should expect to need additional flips (plus the one we just “spent”).

That is,

Solving yields .  More generally, if P(success) is , the expected number of trials until the first success is .

Solution

We can apply this same idea to Chutes and Ladders.  Let be the expected number of turns needed to finish the game (i.e., reach square 100), starting from square , where (so that is the value we really want).  Then

where is the number of the square reached from square by rolling — which is usually just equal to , but this function also “encodes” the configuration of chutes and ladders on the board, as well as the requirement of landing exactly on square 100 to end the game.

So we have a system of 100 linear equations in 100 unknowns, which we can now talk the computer into solving for us (in Python):

import numpy as np

n, m = 100, 6
chutes = {1: 38, 4: 14, 9: 31, 16: 6, 21: 42, 28: 84, 36: 44,
          48: 26, 49: 11, 51: 67, 56: 53, 62: 19, 64: 60, 71: 91,
          80: 100, 87: 24, 93: 73, 95: 75, 98: 78}

A = np.eye(n)
b = np.ones(n)
for i in range(n):
    for j in range(1, m + 1):
        k = i if i + j > n else chutes.get(i + j, i + j)
        if k < n:
            A[i][k] -= 1.0 / m
x = np.linalg.solve(A, b)

Results

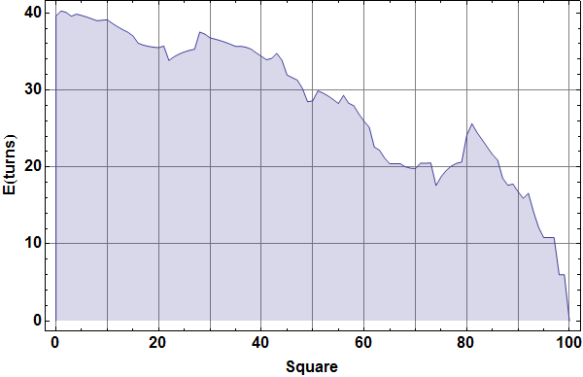
The following figure shows all of the resulting values .  For example, the expected number of turns to complete the game from the start is .

Expected number of (additional) turns to finish game starting from the given square.

Note that we can easily analyze the “house rule” used in the DataGenetics post– allowing a player to win even when “overshooting” square 100– simply by changing the k=i in line 12 to k=n.  The result is a modest reduction in game length, to about 36.1931 turns.  (Edit: However, this is not the whole story.  See this subsequent post addressing the fact that the game involves multiple players.)

References:

1. Althoen, S. C., King, L., and Schilling, K., How Long Is a Game of Snakes and Ladders?  The Mathematical Gazette, 77(478) March 1993, p. 71-76 [JSTOR]
2. DataGenetics blog, Mathematical Analysis of Chutes and Ladders [HTML]
3. Hochman, M., Chutes and Ladders [PDF]