Probability of a Scrabble bingo

My wife and I have been playing Scrabble recently.  She is much better at the game than I am, which seems to be the case with most games we play.  But neither of us are experts, so that bingos— playing all 7 tiles from the rack in a single turn, for a 50-point bonus– are rare.  I wondered just how rare they should be… accounting for the fact that I am a novice player?

Let’s focus the problem a bit, and just consider the first turn of the game, when there are no other tiles on the board: what is the probability that 7 randomly drawn Scrabble tiles may be played to form a valid 7-letter word?

There are , or over 16 billion equally likely ways to draw a rack of 7 tiles from the 100 tiles in the North American version of the game.  But since some tiles are duplicated, there are only 3,199,724 distinct possible racks (not necessarily equally likely).  Which of these racks form valid words?

It depends on what we mean by valid.  According to the 2014 Official Tournament and Club Word List (the latest for which an electronic version is accessible), there are 25,257 playable words with 7 letters… but many of those are words that I don’t even know, let alone expect to be able to recognize from a scrambled rack of tiles.  We need a way to reduce this over-long official list of words down to a “novice” list of words– or better yet, rank the entire list from “easiest” to “hardest,” and compute the desired probability as a function of the size of the accepted dictionary.

The Google Books Ngrams data set (English version 20120701) provides a means of doing this.  As we have done before (described here and here), we can map each 7-letter Scrabble word to its frequency of occurrence in the Google Books corpus, the idea being that “easier” words occur more frequently than “harder” words.

The following figure shows the sorted number of occurrences of all 7-letter Scrabble words on a logarithmic scale, with some highlighted examples, ranging from between, the single most frequently occurring 7-letter Scrabble word, to simioid, one of the least frequently occurring words… and this doesn’t even include the 1444 playable words– about 5.7% of the total– that appear nowhere in the entire corpus, such as abaxile and zygoses.

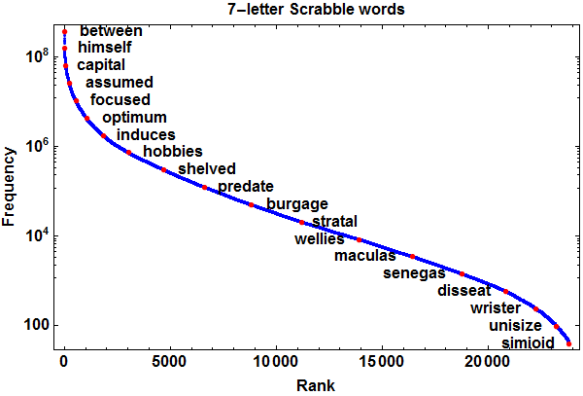
Scrabble 7-letter words ranked by frequency of occurrence in Google Books Ngrams data set.  The least frequent word shown here that I recognize is “predate.”

Armed with this sorted list of 25,257 words, we can now compute, as a function of , the probability that a randomly drawn rack of 7 tiles may be played to form one of the easiest words in the list.  Following is Mathematica code to compute these probabilities.  This would be slightly simpler– and much more efficient– if not for the wrinkle of dealing with blank tiles, which allow multiple different words to be played from the same rack of tiles.

tiles = {" " -> 2, "a" -> 9, "b" -> 2, "c" -> 2, "d" -> 4, "e" -> 12,
   "f" -> 2, "g" -> 3, "h" -> 2, "i" -> 9, "j" -> 1, "k" -> 1, "l" -> 4,
   "m" -> 2, "n" -> 6, "o" -> 8, "p" -> 2, "q" -> 1, "r" -> 6, "s" -> 4,
   "t" -> 6, "u" -> 4, "v" -> 2, "w" -> 2, "x" -> 1, "y" -> 2, "z" -> 1};

{numBlanks, numTiles} = {" " /. tiles, Total[Last /@ tiles]};

racks[w_String] := Map[
  StringJoin@Sort@Characters@StringReplacePart[w, " ", #] &,
  Map[{#, #} &, Subsets[Range[7], numBlanks], {2}]]

draws[r_String] :=
 Times @@ Binomial @@ Transpose[Tally@Characters[r] /. tiles]

all = {};
p = Accumulate@Map[(
       new = Complement[racks[#], all];
       all = Join[all, new];
       Total[draws /@ new]
       ) &,
     words] / Binomial[numTiles, 7];

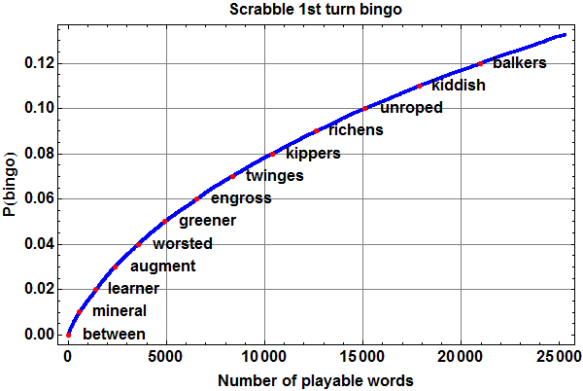
The results are shown in the following figure, along with another sampling of specific playable words.  For example, if we include the entire official word list, the probability of drawing a playable 7-letter word is 21226189/160075608, or about 0.132601.

Probability that 7 randomly drawn tiles form a word, vs. dictionary size.

A coarse inspection of the list suggests that I confidently recognize only about 8 or 9 thousand– roughly a third– of the available words, meaning that my probability of playing all 7 of my tiles on the first turn is only about 0.07.  In other words, instead of a first-turn bingo every 7.5 games or so on average, I should expect to have to wait nearly twice as long.  We’ll see if I’m even that good.