In [3], Peter Winkler lists “seven problems you think you must not have heard correctly.” I think the following problem deserves to be on such a list:
Alice and Bob are playing a game, searching bins arranged in a grid with 
Alice decides to systematically search the grid row by row, left to right across each row, from the top row to the bottom. Bob decides to search columns, top to bottom, left to right. Which player is more likely to win? What if instead the game is played– using the same strategies above– on a slightly wider grid with 
I really like this problem, since a natural reaction might be, “How can either player possibly have an advantage?” (And for just 
// Compute probability Alice wins by searching rows.
Rational p_grid_search_rows(int rows, int cols, int balls) {
int ai = 1, aj = 0, bi = 0, bj = 0; // start in upper left
Integer wins = 0;
// Evaluate each bin/time where Alice finds a ball first.
for (int bin = 1; bin <= rows * cols; ++bin) {
if (++bi == rows) { bi = 0; ++bj; } // move Bob down
if (bin < aj * rows + ai) { // verify Alice got here first
// Place remaining balls in unsearched bins.
int searched = 2 * bin - ai * bj - std::min(ai, bi);
wins += binomial(rows * cols - searched, balls - 1);
}
if (++aj == cols) { aj = 0; ++ai; } // move Alice right
}
return Rational(wins, binomial(rows * cols, balls));
}
The result is that for the original problem with 
The figure below shows that it’s more complicated than this, though, indicating which player has the advantage as we vary the grid size, keeping the number of balls
with balls.I first encountered this problem in [1] and [2], where the problem is generalized to consider search strategies as arbitrary permutations of the bins.
References:
Possibly Wrong 
I as thinking about how to intuit the initially-surprising advantage by thinking at the extremes. Imagine rows=2 and cols=1e9 (or any large number) grid. Setting aside the first and last turns, for the first half of the game Alice spends half her turns exploring space already explored by Bob, effectively passing half her turns, while Bob explores new bins every turn. At the game’s halfway point Bob stops exploring any new territory, effectively passing the entire second half of the game. They’re the first to the same number of bins, but Bob visits his half sooner.
At K=1, it’s just a coin flip whether that ball is in an Alice bin or a Bob bin. At K>1, and balls are evenly split, as they are on average, Bob tends to find his sooner.
Yep, this is where that intuitive argument is cleanest; in particular for two rows and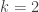
, it’s a not-too-bad exercise to show that the limiting probability that Alice wins approaches 5/8 as the number of columns grows large. (I think the players are reversed in your description; note that Alice searches the top row, then the second row, etc., so that she has the advantage, not Bob, for a 2-by-many-columns grid.)
This is pretty unintuitive, largely I think because nobody would actually play this way. In an actual game, why would Bob choose a bin that Alice had already picked? Do they not know which bins were selected previously? Or the obvious strategy of their opponent?
Agree that the “dressing” on the problem setup is sketchy– since if players always avoid bins that they have observed to already be searched, then the problem is no longer interesting enough to be a problem, in that the only advantage of the first player is in moving first, independent of the order in which unexplored bins are chosen.
Another way I have seen this problem presented is for Alice to “go first,” exploring until she finds a ball, but without Bob watching the process. Then Bob takes his turn, unaware of which bins were already searched by Alice. Whoever takes the least time– more precisely, the fewest number of searched bins– to find a ball wins. Same problem, different dressing.
Pingback: 网格搜索——直觉往往不那么准确 – Sqr5's blog