Exact analysis of Dreidel game

Introduction

A few weeks ago I read an interesting article by Hillel Wayne [6], discussed on Hacker News, describing analysis of Dreidel, a game traditionally played during the Jewish holiday of Hanukkah. Each player starts with the same number of tokens– often foil-wrapped chocolate coins– and antes one coin each into the center pot. Players take turns spinning the dreidel, with one of four equally likely outcomes:

• Nun (“nothing”): player does nothing, turn passes to next player on the left.
• Gimel (“everything”): player takes all of the coins in the pot. With the pot now empty, everyone, including the current player, antes one coin back into the pot.
• Hei (“half”): player takes half of the coins in the pot. If there are an odd number of coins in the pot, the player rounds up, taking the larger half. If this empties the pot, i.e. if only one coin was in the pot, everyone– again including the current player– must ante one coin back into the pot.
• Shin (“put”): player puts one coin into the pot.

A player is out of the game if they cannot put a coin into the pot when required. Play continues until one player remains, who wins all of the coins.

The motivation for this post is to try to improve upon past analyses of Dreidel, which involve various limitations, simplifying assumptions, and/or approximations in their solution; and to present exact probabilities and expected values for the game, that raise an interesting conjecture that appears to be new. The Python code is available on GitHub.

Another token-passing game

What initially caught my attention to this problem was how much it has in common with the Left-Center-Right dice game discussed in the previous post. Both Dreidel and Left-Center-Right are “games” with no strategy, with all “moves” dictated solely by the random outcome of a spin/roll. Both games involve passing tokens (coins) around among the players and a center pot, with the game ending with one player winning all of the coins.

We can thus apply essentially the same method to analyzing Dreidel, solving a sequence of linear systems of equations, indexing matrix rows and columns by ranking corresponding weak compositions of the coins in play… but with one modification. In Left-Center-Right, the number of players remains fixed throughout the game, but the number of coins in circulation is always decreasing; once a coin enters the pot, it stays there. In Dreidel, the opposite is true: all of the coins remain in circulation throughout the game, entering and leaving the pot, but the number of players decreases as players go “out” when they are unable to put a coin into the pot. Thus, in Dreidel the sequence of linear systems is indexed by the changing number of players, instead of by number of coins.

(As an aside, since I’m always on the lookout for nice exercises for students in mathematics or computer science: show that this same row/column indexing approach used in Left-Center-Right isn’t “wasteful” when applied to Dreidel. That is, show that every distribution of coins among the players, with a positive number of coins in the pot, is a reachable state of the game.)

Rule variations

Although this analysis assumes the specific rules of the game as described above, there are several variations supported in the Python code. For example, the article [6] that motivated this post seems unique in specifying min_coins=1, requiring players to always have a positive minimum number of coins, going out immediately if they ever have zero coins. We instead follow the convention assumed in all of the other references that min_coins=0: a player is only out when they can’t pay.

Another variation deals with taking half the pot when there are an odd number of coins. Robinson and Vijay [4] specify half_odd=0, rounding down, with the player taking the smaller half of the pot; but we follow the elsewhere-convention of half_odd=1, rounding up.

Results and conjecture

References [1] and [4] observe that Dreidel takes a long time to play, with a number of spins that varies (at most) quadratically as the number of players. The exact expected length of the game is shown in the figure below.

Expected number of turns (i.e., dreidel spins) and hours to complete a game, vs. number of coins each player starts with.

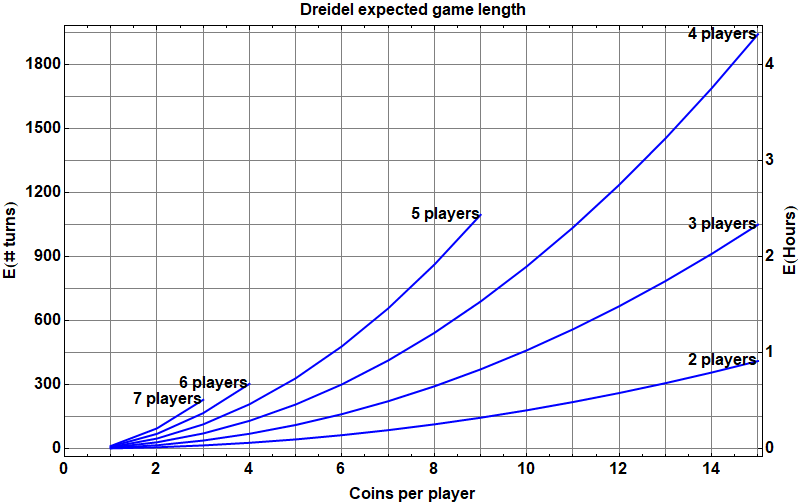
Assuming 8 seconds per spin as in [1], a four-player game would take almost 2 hours on average to complete if each player starts with 10 coins, and nearly 4.5 hours if each player starts with 15 coins.

What I found most interesting about Dreidel, however, is how the advantage varies with player position. All of the references below suggest that the first player to spin has an advantage (although based on simulation and/or various simplifying approximations), and that things get worse as we move around the table, with the last player to spin having the least probability of winning.

But if we compute these probabilities exactly, and present results as the expected return, or the average number of coins “gained” relative to initial wagered coins at the start of the game, we see the following interesting behavior:

Expected net coins won vs. number of starting coins wagered, for the starting player (blue) and for the last player (red).

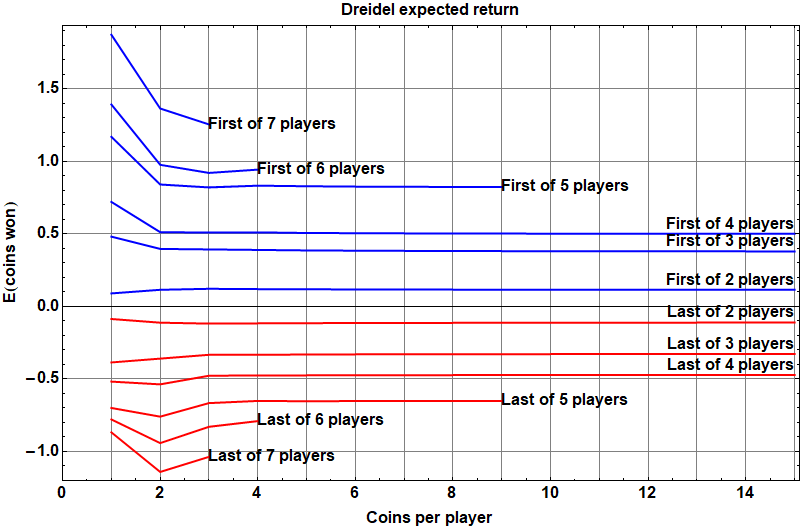
I’ve sacrificed completeness to try to preserve clarity, only showing the first player’s return in blue, and the last player’s in red; the other players’ returns vary monotonically between these two extremes.

This figure suggests that a player’s expected return seems to very quickly approach a non-zero limit as the starting number of coins increases, that depends on the position of the player around the table. For example, in a game with four players, the first player to spin can expect to net about half a coin per game, no matter whether the players start with 2 coins each or 15, while the last player can expect to lose about half a coin per game.

References:

1. Blatt, B., Dreidel: The classic Hannukah game is painfully slow. It’s time to speed it up, Slate, December 2014 [HTML]
2. Feinerman, R., An Ancient Unfair Game, The American Mathematical Monthly, 83(8) October 1976, p. 623-625 [JSTOR]
3. Lucas, S., Who wins when playing Dreidel, 2nd Mathematics Of Various Entertaining Subjects (MOVES) Conference, Museum of Mathematics, New York, August 2015 [PDF]
4. Robinson, T. and Vijay, S., Dreidel lasts spins, Advances in Applied Mathematics, 36(1) January 2006, p. 85-94 [arXiv]
5. Trachtenberg, F., The Game of Dreidel Made Fair, The College Mathematics Journal, 27(4) September 1996, p. 278-281 [JSTOR]
6. Wayne, H., I formally modeled Dreidel for no good reason [HTML]