A few weeks ago, I learned that my niece and nephew enjoy playing the board game Monopoly. Around that same time, I read a recent blog post on God Plays Dice wondering about the expected net amount of money a player “earns” each trip around the board (from passing Go, paying income/luxury tax, etc.). This got me thinking about re-visiting my past analysis of the game.
(Does anyone actually enjoy playing Monopoly anymore? Given that it seems to be one of the most tedious-yet-popular, hated-but-played-anyway board games of the past century, I would have guessed that anyone who hasn’t already stopped reading at this point must be at least my age or older. But my niece and nephew are not even 12 years old, and apparently love the game. Go figure.)
Monopoly has been modeled, simulated, and analyzed before… a lot. (See the references at the end of this post, by no means a complete list.) I remember first reading about the potential to apply interesting mathematics to the game in 1996, in Ian Stewart’s Mathematical Recreations column in Scientific American (7 and 8). The basic idea has been refined and re-applied many times: a player’s travels around the board may be modeled as a Markov chain, with each state corresponding to the player’s position (i.e., square) on the board, and the matrix of transition probabilities corresponding to the roll of the dice, the random drawing of Chance and Community Chest cards, etc. Armed with this transition matrix, we can compute the steady-state distribution, or the limiting frequency with which a player lands on each of the squares on the board (more on this later).
This straightforward analysis is complicated somewhat by two aspects of the game. The first wrinkle is the drawing of Chance and Community Chest cards. The usual means of preserving stationarity is to assume a slight change of rules so that (1) each deck is re-shuffled prior to every draw, and (2) Get Out Of Jail Free cards are never kept when drawn, and are immediately returned to the deck for a $50 credit. With these assumptions, there are always 16 cards in each deck, and a random draw does not depend on any prior draws.
The second wrinkle is the rule for rolling doubles and getting in and out of jail: if you roll doubles you take another turn, except that if you roll 3 doubles in a row you go immediately to jail and lose your turn. Although some early analyses made convenient simplifying assumptions here as well, we can handle this without too much trouble, by expanding the state space to include 3 states for each of the 40 squares on the board, corresponding to having rolled 0, 1, or 2 consecutive doubles. (To model the rule for rolling doubles to get out of jail, when already in jail, the 3 states correspond to not having rolled doubles on the past 0, 1, or 2 consecutive turns.)
For anyone interested in diving into this further, I did the tedious work for you: the 120×120 transition matrices with exact probabilities are at the usual location here.
(Actually, it wasn’t that tedious. Reference 2 suggests that “hundreds of lines” of code are needed, but I’m not sure why. Following is the rather poor Mathematica code, mostly a crude translation from my earlier and even poorer C code, that generates the transition matrices.)
update[{square1_, doubles1_}, {square2_, doubles2_}, p_] :=
P[[3 square1 + doubles1 + 1, 3 square2 + doubles2 + 1]] += p
nextDoubles[rollAgain_] :=
If[die1 == die2 && rollAgain,
If[square == 30, 0, doubles] + 1,
0
]
communityChest[square2_, p_, rollAgain_] :=
(
(* Go to Jail. *)
update[{square, doubles}, {30, 0}, p/16];
(* Advance to Go. *)
update[{square, doubles}, {0, nextDoubles[rollAgain]}, p/16];
(* Stay on Community Chest. *)
update[{square, doubles}, {square2, nextDoubles[rollAgain]}, p*7/8];
)
chance[square2_, p_, rollAgain_] :=
Module[
{square3},
(* Go to Jail. *)
update[{square, doubles}, {30, 0}, p/16];
(* Go back 3 spaces. *)
square3 = Mod[square2 - 3, 40];
If[square3 == 33,
communityChest[square3, p/16, rollAgain],
update[{square, doubles}, {square3, nextDoubles[rollAgain]}, p/16]
];
(* Advance to Go. *)
update[{square, doubles}, {0, nextDoubles[rollAgain]}, p/16];
(* Advance to nearest railroad. *)
square3 = Switch[square2, 7, 15, 22, 25, _, 5];
update[{square, doubles}, {square3, nextDoubles[rollAgain]}, p/8];
(* Take a ride on the Reading. *)
update[{square, doubles}, {5, nextDoubles[rollAgain]}, p/16];
(* Advance to St. Charles Place. *)
update[{square, doubles}, {11, nextDoubles[rollAgain]}, p/16];
(* Advance to the nearest utility. *)
square3 = If[square2 == 22, 28, 12];
update[{square, doubles}, {square3, nextDoubles[rollAgain]}, p/16];
(* Advance to Illinois Avenue. *)
update[{square, doubles}, {24, nextDoubles[rollAgain]}, p/16];
(* Advance to Boardwalk. *)
update[{square, doubles}, {39, nextDoubles[rollAgain]}, p/16];
(* Stay on Chance. *)
update[{square, doubles}, {square2, nextDoubles[rollAgain]}, p*3/8]
]
advance[rollAgain_] :=
Module[
{square3},
(* Move to new position. *)
square3 = Mod[If[square == 30, 10, square] + die1 + die2, 40];
Switch[square3,
(* Go to Jail. *)
30, update[{square, doubles}, {30, 0}, 1/36],
(* Draw a Chance card. *)
7 | 22 | 36, chance[square3, 1/36, rollAgain],
(* Draw a Community Chest card. *)
2 | 17 | 33, communityChest[square3, 1/36, rollAgain],
(* Move to new position. *)
_, update[{square, doubles}, {square3, nextDoubles[rollAgain]}, 1/36]
]
]
transitionMatrix[getOutOfJail_] :=
(
(* Initialize transition matrix. *)
P = Table[0, {120}, {120}];
(* Compute each row of transition matrix. *)
Do[
If[square == 30,
(* We are in Jail. *)
If[getOutOfJail || die1 == die2 || doubles == 2,
advance[getOutOfJail],
update[{square, doubles}, {square, doubles + 1}, 1/36]
],
(* We are not in Jail. Go to Jail if we roll 3 doubles. *)
If[die1 == die2 && doubles == 2,
update[{square, doubles}, {30, 0}, 1/36],
advance[True]
]
],
{square, 0, 39},
{doubles, 0, 2},
{die1, 6}, {die2, 6}
];
P
)
Note that I said, “transition matrices.” There are arguably two distinct classes of strategies in Monopoly, each with a slightly different transition matrix: early in the game, you play the “Get Out Of Jail” strategy, paying the $50 to get out of jail immediately to visit and purchase as many properties as possible. Late in the game, however, it makes sense to “Stay In Jail” as long as possible, collecting rent from your opponent while not risking paying rent yourself.
In either case, given the transition matrix 
Butler and Pratt (references 2 and 6) provide tables showing the resulting limiting frequencies of landing on a square on any given turn, along with several other statistics derived from this basic calculation.
Except that this analysis has always bothered me. Computing the steady-state distribution is the “nugget” of neat mathematics applied to this problem. The fact that we can understand a board game by solving a linear algebra problem certainly has some appeal of elegance. But how accurate is it? Specifically, how quickly does the Markov chain converge to the steady-state distribution, compared with the number of dice rolls in an actual typical game of Monopoly?
There are several interesting studies of this. As a first approximation, consider the expected number of rolls needed to simply visit all property squares at least once. If we suppose that every property is bought as soon as it is landed on, then this is an estimate of how long players use the “Get Out Of Jail” strategy in the first stage of the game.
Pratt suggests that this expected number of rolls is 50; however, he (incorrectly) computes this value as the least number of rolls such that the expected number of visits to each property square is at least 1, which is not quite the same thing. We can do better by actually simulating the game. Since we are only interested in visiting properties (vs. purchasing and building on them, collecting and paying rent, etc.), this is easy to do using the transition matrix. Following is Mathematica code and the resulting distribution of number of rolls needed in a two-player game:
simulate[numPlayers_, P_] :=
Module[
{
players = Table[1, {numPlayers}],
rolls = Table[0, {numPlayers}],
turn = 1,
remaining = {2, 4, 6, 7, 9, 10, 12, 13, 14, 15, 16, 17, 19, 20, 22,
24, 25, 26, 27, 28, 29, 30, 32, 33, 35, 36, 38, 40},
s
},
While[remaining =!= {},
s = RandomChoice[P[[players[[turn]]]] -> Range[120]];
players[[turn]] = s;
rolls[[turn]] = rolls[[turn]] + 1;
If[Mod[s, 3, 1] < 2, turn = Mod[turn + 1, numPlayers, 1]];
remaining = Complement[remaining, {Ceiling[s/3]}]
];
rolls
]
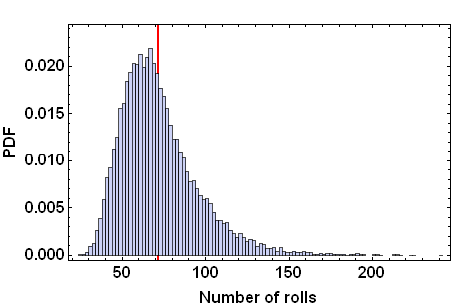
Distribution of number of rolls needed to visit all properties in 2-player game. The mean (shown in red) is approximately 72 rolls.
More detailed analyses are presented by Frayn and Friedman that are consistent with these results, but with an additional interesting observation: most games never reach the second stage where players might use the “Stay In Jail” strategy… or if they do, then they are likely to go on forever! Friedman “confirmed that, in fact, the potential for the game ending after Stage 2 is reached is very slight” (5). So it seems that we can focus our attention on the “Get Out Of Jail” strategy; as Frayn (4) puts it:
It is almost always a wise idea to pay to get out of jail. If you get to the point when you are staying in jail to avoid paying rent then you’ve probably lost anyway!
Getting back to the steady-state distribution again, how accurately does it estimate frequencies of visiting squares on the board, given that a typical two-player game lasts for less than 100 rolls per player? To answer this question, I think it is important to emphasize a distinction that is missed in some previous analyses. Specifically, we really care about the expected number of visits to each property over the course of the game, not just the probability of visiting each property on a given turn. In other words, in a game where a player rolls the dice 
as opposed to just
where 
Note that if we are only interested in steady-state behavior, then this distinction doesn’t really matter, since both of these expressions converge to the steady-state distribution as 
If we “collapse” these frequencies by considering properties in the same color group together, then the differences are less extreme. The following Figure (a) shows the “actual” relative frequencies of landing on the various property color groups (i.e., for reasonable numbers of rolls), compared with Figure (b) showing the corresponding steady-state distribution. The only change in order statistics is that the light purple group (St. Charles Place, States Ave., and Virginia Ave.) is actually slightly more frequently visited than the green group (Pacific Ave., North Carolina Ave., and Pennsylvania Ave.).
(a) Frequency of landing on property color groups in the first 72 rolls. (b) Limiting frequencies based on steady-state distribution.
References:
- Ash, R. and Bishop, R., Monopoly as a Markov Process. [PDF]
- Butler, B., Durango Bill’s Monopoly Probabilities. [HTML]
- Collins, T., Probabilities in the game of Monopoly. [HTML]
- Frayn, C., An Evolutionary Approach to Strategies for the Game of Monopoly, IEEE Symposium on Computational Intelligence and Games (2005). [PDF]
- Friedman, E. et. al., Estimating the Probability That the Game of Monopoly Never Ends, Proceedings of the 2009 Winter Simulation Conference, 380-391. [PDF]
- Pratt, R., Monopoly as a Markov Process, OR 389 Student Seminar Notes. [HTML]
- Stewart, I., How fair is Monopoly? Scientific American, 274 (April 1996):104-105.
- Stewart, I., Monopoly Revisited, Scientific American, 275 (October 1996):116–119.
Possibly Wrong 