Projectile motion puzzle

This problem is inspired by Jackie Bradley, Jr., outfielder for the Boston Red Sox, who last week in warm-up threw a baseball from near home plate over the 17-feet-high wall in deep center field, 420 feet away.  (Here is a video clip of the throw.)

It’s a pretty amazing throw… but just how amazing is it?  That is, how hard would you have to throw a baseball to clear a 17-foot wall 420 feet away?

This is an interesting question in its own right, with the usual appeal of encouraging both pen-and-paper as well as computer simulation for a solution.  I’ll get to the answer shortly– but while working on it, I encountered an interesting relationship between some of the variables that has a nice geometric interpretation, which I think is best illustrated with the following slightly different version of the problem:

Problem: Suppose that you are standing on the outer bank of a moat surrounding a castle, and you wish to secretly deliver a message, attached to a large rock, to your spy inside the castle.  A wall h=11 meters high surrounds the castle, which is in turn surrounded by the moat which is d=19 meters wide.  At what angle should you throw the rock in order to have the best chance of clearing the wall?

At what angle should you throw an object to clear a wall 19 meters away and 11 meters high?

The intent of the large rock is to allow us to ignore the relatively negligible effects of air resistance, thus preventing the calculus problem from becoming a differential equations problem.

We can’t afford to do that with a baseball, though.  Coming back to the original problem at Fenway Park, there are two important atmospheric effects to consider.  First, air resistance significantly increases the speed at which Bradley must have thrown the ball to clear the outfield wall.  But second, the Magnus force resulting from backspin on the ball (also responsible for curve balls and surprisingly hard-to-catch pop-ups) actually makes the ball travel farther, thus decreasing the required speed compared with a ball thrown with no backspin.

Accounting for both of these effects, by my calculations (which I can share if there is interest), Bradley would have had to throw the ball at over 105 miles per hour, at an angle of a little over 30 degrees.

 

Using a watch– or a stick– as a compass

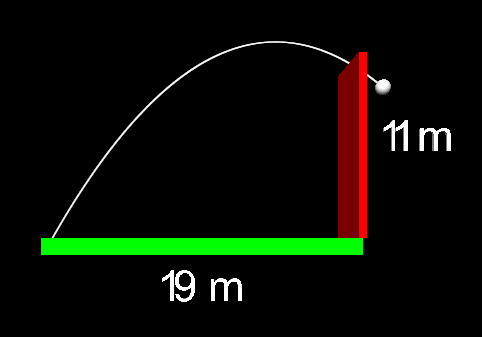
A couple of years ago, I wrote about a commonly cited method of direction-finding using an analog watch and the sun.  Briefly, if you hold your watch face horizontally with the hour hand pointing toward the sun, then the ray halfway between the hour hand and 12 noon points approximately true south.  (This is for locations in the northern hemisphere; there is a slightly different version that works in the southern hemisphere.)

The punch line was that the method can be extremely inaccurate, with errors potentially exceeding 80 degrees depending on the location, month, and time of day.  I provided a couple of figures, each for a different “extreme” location in the United States, showing the range of error in estimated direction over the course of an entire year.

Unfortunately, I ended on that essentially negative note, without considering any potentially more accurate methods as an alternative.  This post is an attempt to remedy that.  In recent discussion in the comments, Steve H. suggested analysis of the use of the “shadow-stick” method: place a stick vertically in the ground, and mark the location on the ground of the tip of the stick’s shadow at two (or more) different times.  The line containing these points will be roughly west-to-east.

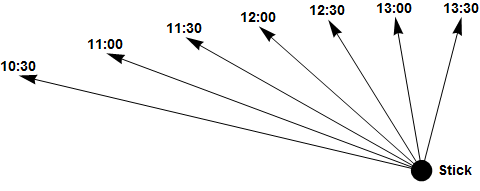
Illustration of the shadow-stick method of direction-finding. With a stick placed vertically in the ground, the tip of the stick’s shadow moves roughly from west to east.

As the following analysis shows, this shadow-stick method of direction-finding is indeed generally more accurate than the watch method… most of the time, anyway.  But even when it is better, it can still be bad.  It turns out that both methods are plagued with some problems, with the not-so-surprising conclusion that if you need to find your way home, there is a tradeoff to be made between accuracy and convenience.

One of the problems with my original presentation was condensing the behavior of the watch method over an entire year into a single plot (in this case, at Lake of the Woods in Minnesota, at a northern latitude where the watch method’s accuracy is best).  This clearly shows the performance envelope, i.e. the maximum possible error over the whole year, but it hides the important trending behavior within each day, and how that daily trend changes very gradually over the year.  We can see this more clearly with an animation: the following shows the same daily behavior of error in estimated direction using the watch method (in blue), but also the shadow-stick method (in red), over the course of this year.

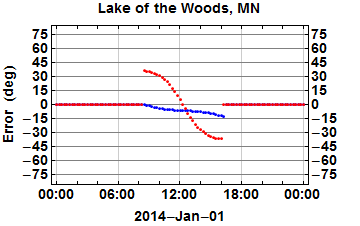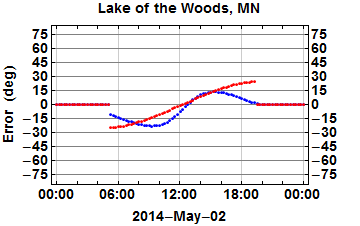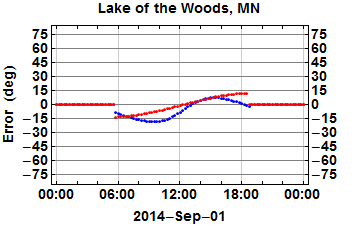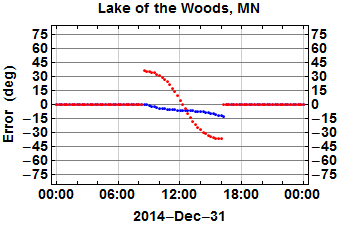
Accuracy of the watch method (blue) and shadow-stick method (red) of direction-finding, over the course of the year 2014 in Lake of the Woods, Minnesota. The shadow-stick method is more accurate 40.6% of the time.

For reference, following are links to a couple of other animations showing the same comparison at other locations.

• Florida Keys (a southern extreme, where the watch method performs poorly, included in the original earlier post)
• Durango, Colorado (discussed in the comments on the earlier post)

There are several things to note here.  First, this is an example where the shadow-stick method can actually perform significantly worse than the watch method.  Its worst-case behavior is near the solstices in June and December, with errors exceeding 30 degrees near sunrise and sunset.  This worst-case error increases with latitude, which is the opposite of how the watch method behaves, as shown by the Florida Keys example above.

However, note the symmetry in the error curve for the shadow-stick method.  It always passes from an extreme in the morning, to zero around noon, to the other extreme in the evening.  We can exploit this symmetry… if we are willing to wait around a while.  That is, we could improve our accuracy by making a direction measurement some time in the morning before noon, then making another measurement at the same time after noon, and using the average of the two as our final estimate.  (A slightly easier common refinement of the shadow-stick method is to (1) mark the tip of the shadow sometime in the morning, then (2) mark the shadow again later in the afternoon when the shadow is the same length.  The basic idea is the same in either case.)

Finally, this issue of the length of time between measurements is likely an important consideration in the field.  A benefit of the watch method is that you get a result immediately; look at the sun, look at your watch, and you’re off.  The shadow-stick method, on the other hand, requires a pair of measurements, with some waiting time in between.  How long are you willing to wait for more accuracy?

Interestingly, the benefit of that additional waiting time isn’t linear– that is, all of the data shown here assumes just 15 minutes between marking the stick’s shadow.  Waiting longer can certainly reduce the effect of measurement error (i.e., the problem of using cylindrical sticks and spherical pebbles, etc., instead of mathematical line segments and points) by providing a longer baseline… but the inherent accuracy of the method only improves significantly when the two measurement times span apparent noon, as in the refinement above, which could take hours.

To wrap up, I still do not see a way to condense this information into a reasonably simple, easy-to-remember, expedient method for finding direction in the field without a compass.  The regular, symmetric behavior of the error in the shadow-stick method suggests that we could possibly devise an “immediate” method of eliminating most of that error, by considering the extent and sense of the error as a function of the season, and a “scale factor” as a function of the time until/since noon… but that starts to sound like anything but “simple and easy-to-remember.”