The Price Is Right puzzle solution

This is just a quick follow-up to capture my notes on an approach to solving the following problem from the last post:

Problem: Suppose you and  other players are playing the following game.  Each player in turn spins a wheel as many times as desired, with each spin adding to the player’s score a random value uniformly distributed between 0 and 1.  However, if a player’s cumulative score ever exceeds 1, she immediately loses her turn (and the game).

After all players have taken a turn, the player with the highest score (not exceeding 1) wins the game.  You get to go first– what should your strategy be, and what are your chances of winning?

Solution: Suppose that our strategy is to continue to spin until our score exceeds some target value .  The first key observation is that the probability that we do so “safely,” i.e. reach a total score greater than without exceeding 1, is

To see this, partition the successful outcomes by the number of initial spins with total score at most , with the final -st spin landing the total score in the interval .  The probability of such an outcome is

(which may be shown by induction, or see also here and here), and the result follows from the Taylor series expansion for .

At this point, we can express the overall probability of winning using strategy as

Intuitively, we must:

1. Safely reach a score in the interval , with probability ; and
2. For each such score , reached with uniform density , each of the remaining players must fail to beat our score.

The optimal strategy consists of choosing a target score maximizing .  Unfortunately, this does not have a closed form; however, after differentiating and some manipulation, the desired target score can be shown to be the root in of the following equation, which has a nice interpretation:

The idea is that we are choosing a target score where the (left-hand side) probability of winning by spinning one more time exactly equals the (right-hand side) probability of winning by stopping with the current score .

Handing the problem over to the computer, the following table shows the optimal target score and corresponding probability of winning for the first few values of .

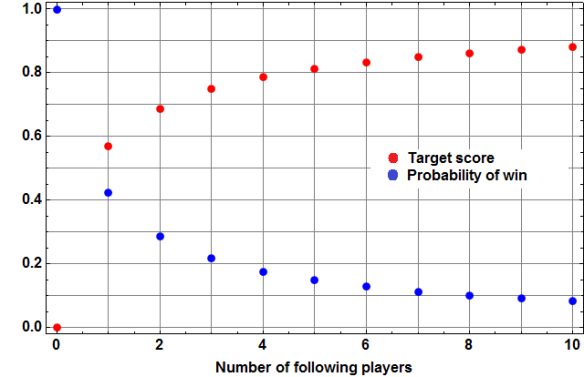
Optimal target score (red) and corresponding probability of winning (blue), vs. number of additional players.

One final note: how does this translate into an optimal strategy for the players after the first?  At any point in the game, the current player has some number of players following him.  His optimal strategy is to target the maximum of the best score so far from the previous players, and the critical score computed above.

[Edit: Following is Python code using mpmath that implements the equations above.]

import mpmath

def q(t):
    return mpmath.exp(t) * (1 - t)

def p_stop(t, n):
    return (1 - q(t)) ** n

def p_spin(t, n):
    return mpmath.quad(lambda s: p_stop(s, n), [t, 1])

def t_opt(n):
    return mpmath.findroot(
        lambda t: p_spin(t, n) - p_stop(t, n), [0, 1], solver='ridder')

def p_win(t, n):
    return q(t) / (1 - t) * p_spin(t, n)

if __name__ == '__main__':
    for n in range(11):
        t = float(t_opt(n))
        p = float(p_win(t, n))
        print('{:4} {:.9f} {:.9f}'.format(n, t, p))

 

The Price Is Right… sort of

After a couple of recent conversations about the dice game puzzle proposed a few months ago, I spent some time experimenting with the following game that has a vaguely similar “feel,” and that also has the usual desirable feature of being approachable via either computer simulation or pencil and paper.

Suppose you and n other players are playing the following game.  Each player in turn spins a wheel as many times as desired, with each spin adding to the player’s score a random value uniformly distributed between 0 and 1.  However, if a player’s cumulative score ever exceeds 1, she immediately loses her turn (and the game).

After all players have taken a turn, the player with the highest score (not exceeding 1) wins the game.  You get to go first– what should your strategy be, and what are your chances of winning?

The obvious similarity to the dice game Pig is in the “jeopardy”-type challenge of balancing the risk of losing everything– in this case, by “busting,” or exceeding a total score of 1– with the benefit of further increasing your score, and thus decreasing the other players’ chances of beating that score.

I like this “continuous” version of the problem, for a couple of reasons.  First, it’s trickier to attack with a computer, resisting a straightforward dynamic programming approach.  But at the same time, I think we still need the computer, despite some nice pencil-and-paper mathematics involved in the solution.

We can construct an equally interesting discrete version of the game, though, as well: instead of each spin of the wheel yielding a random real value between 0 and 1, suppose that each spin yields a random integer between 1 and m (say, 20), inclusive, where each player’s total score must not exceed m.  The first player who reaches the maximum score not exceeding m wins the game.

This version of the game with n=3 and m=20 is very similar to the “Showcase Showdown” on the television game show The Price Is Right, where three players each get up to two spins of a wheel partitioned into dollar amounts from $.05 to $1.00, in steps of $.05.  The television game has been analyzed before (see here, for example), but as a computational problem I like this version better, since it eliminates both the limit on the number of spins, as well as the potential for ties.