Playing the subtraction game with GPT-4

Does GPT-4 exhibit “intelligence,” or is it simply a sophisticated stochastic parrot? This is a fun polarizing question to ask at your next cocktail party of machine learning researchers, linguists, hackers, and philosophers. This post is motivated by recent similar questions I have been asked from friends about GPT-4 (along with, “Can I use it to help with my math homework?”).

I don’t think my own opinions here are terribly interesting. Instead, following is a transcript of a recent conversation I had with GPT-4, that I think illustrates in a simple way some of what makes this a polarizing subject. In this conversation, we challenge GPT-4 to a two-player game, and GPT-4 loses. What is interesting here is not that GPT-4 seems to “get it wrong”– humans get it wrong all the time, too– but how it gets it wrong.

Start of transcript

Me: Let’s play a two-player game. We will start with 15 stones. At each turn, a player may remove 1, 2, or 3 stones. The player who removes the last stone loses the game. You go first.

(Aside: This is the “subtraction game,” a very simplified form of Nim… but with a seemingly minor twist: in the “normal” form of the game, the objective is to win by making the last legal move, that is, by taking the last stone. Here, we are playing the misère form of the game, where the objective is to force your opponent to take the last stone.)

GPT-4: Sure, I’d love to play this game with you. Given that we have 15 stones and we can remove between 1 to 3 stones per turn, I understand that the goal is not to take the last stone. Therefore, I’ll start by taking 2 stones.

Now we have 13 stones left. Your turn!

(Aside: The reader can verify that, by starting the game with 15 stones, we effectively offered GPT-4 the opportunity to win by making the first move… and that it made the correct initial move by taking 2 stones. At this point, no matter what we do, GPT-4 has a winning strategy.)

Me: I take 2 stones.

GPT-4: Great! Now there are 11 stones left. I’ll take 1 stone.

So we have 10 stones left now. Your turn!

(Aside: This is a mistake by GPT-4; the optimal move at this point was to take 2 stones, not just 1. From this point on, we have won the game.)

Me: I take 1 stone. After making your next move, can you describe your strategy, and your evaluation of the current state of the game, in particular who you predict can win the game?

GPT-4: Sure, you’ve taken 1 stone, so now we have 9 stones left. I’ll take 3 stones.

Now we have 6 stones left.

Regarding my strategy, I aim to keep the number of stones at multiples of 4 at the end of my turns. This is because if we have a multiple of 4 stones, no matter how many stones (1, 2, or 3) the other player picks, I can always pick a number that brings the total taken by both of us in that round to 4. This means that if I can maintain this pattern, I can ensure that I’m not the one to pick the last stone [my emphasis added].

For example, if we have 4n stones left and the other player picks 3, I can pick 1 to keep the number of stones at 4(n-1). If they pick 2, I can pick 2, and if they pick 1, I can pick 3.

By removing 3 stones from the 9, I have forced the game into this pattern, since 6 is a multiple of 4 [my emphasis added]. At this point, as long as I can maintain this strategy, I should win the game. Now it’s your turn!

Me: I take 1 stone.

GPT-4: You’ve taken 1 stone, so now there are 5 stones left. I will take 3 stones.

Now we have 2 stones left, it’s your turn. Remember, the player who takes the last stone loses.

Me: I take 1 stone.

GPT-4: You’ve taken 1 stone, so now there is only 1 stone left. According to our rules, I must take at least 1 stone, which would be the last one, thus making me lose the game.

Congratulations! You’ve won the game. I hope you enjoyed playing. Would you like to play again or perhaps try a different game?

End of transcript

This is nothing new. It’s well known that GPT-4 hallucinates, and it’s almost a parlor game at this point to come up with puzzles and problems that GPT-4 stumbles over. But I like the subtraction game as an educational example. As with any two-player game of perfect information, it’s approachable in principle by brute-force tree search (think “computer science problem”), that would seem to require “look ahead” planning and reasoning to deduce optimal strategy. But the game has additional structure that makes optimal strategy very simple to characterize and concisely describe (think “mathematics problem”), even for instances of the game with a very large tree– that is, even starting with a very large number of stones. As GPT-4 suggests, adding multiples of 4 stones doesn’t change the eventual outcome. But the devil is in the logical details: we don’t want to end our move with a multiple of 4 stones, as in normal play; instead, we want to end our move with a number of stones that is one more than a multiple of 4.

When GPT-4 makes this mistake, and even confidently persists in justifying the mistake, is this a planning problem, illustrating that GPT-4 is “thinking” but has difficulty with reasoning that requires looking ahead, counterfactuals, etc.? Or is it an illustration of the claim that GPT-4 is essentially just “parroting” the statistically most likely sequence of tokens from its training data, e.g., is discussion of normal play more common than misère play in literature?

The friendship paradox: expectation vs. probability

Introduction

The friendship paradox is often summarized as, “Your friends (probably) have more friends than you do.” This is catchy, probably because of its vaguely insulting feel rather than in spite of it. Better yet, it’s (probably) true. But that “probably” modifier deserves clarification that it doesn’t always get.

I like this result because it makes for a nice graph theory problem. Let’s model a network of friends as a simple undirected graph , with a vertex for each person, and an edge between a pair of vertices representing the (symmetric) friendship relation.

Proof sketch

The argument for the friendship paradox goes something like this: consider a randomly selected person, we’ll call him Victor, represented by vertex in the graph . How many friends does Victor have? This “friend count” is

where and are the degree and neighborhood, respectively, of vertex .

How many friends do Victor’s friends have? Let’s measure this as the mean of the friend counts of Victor’s friends:

(At this point, we must restrict our attention to graphs without isolated vertices– i.e., no friendless people– so that all vertex degrees are non-zero.)

Now, define the random variable to be the “surplus friend count,” that is, the difference between Victor’s friend count and his friends’ average friend count:

Then it’s a nice exercise for the reader to show that , with equality only when every component of is regular, that is, when everyone in a connected component has exactly the same number of friends. (To see this, note that the first term summing the degrees counts each edge exactly twice, and summing the second term contributes for each edge .)

In other words, in any friendship network with variable friend counts, the average surplus friend count is negative.

Expectation vs. probability

So suppose you are at a party, and Alice mentions the friendship paradox, and offers to make a friendly wager with Bob that he has fewer Facebook friends than his Facebook friends do (on average). Is this a good bet?

Before addressing this question, it’s worth noting that the argument presented above differs slightly from Feld’s original 1991 paper [1], Wikipedia, and this recent article that motivated this post. Here we are selecting a vertex at random, and computing the surplus friend count for that specific vertex; where the latter compute an overall average friends’ friend count in a different way, by effectively selecting an edge— and then an endpoint of that edge– at random.

The inequality still holds in either case, but I like the above approach better, since it more easily allows us to re-state the problem in terms of probability instead of expected value. That is, what have we really shown with the above argument? We have not shown that “your friends probably have more friends than you.” That would be a statement about the probability . But all that we have shown is that (assuming variable friend counts), which at best implies, via the pigeonhole principle, that there exists at least one person whose friends have more friends than they do.

In other words, although the expected value of is always negative for any graph (again, with variable friend counts), the probability can vary depending on the structure of the particular graph being considered. And that probability, not the overall expected value, dictates Alice’s advantage in her wager.

The recent paper by Cantwell et. al. in [2] investigates this further, computing the probability and even the entire distribution of for a variety of random graph models as well as real-world social networks. And Alice’s bet? In 2011, Ugander et. al. in [3] evaluated the graph of Facebook friends, and estimated to be about 0.927, indeed a pretty safe bet.

References:

1. Feld, Scott L., Why Your Friends Have More Friends Than You Do, American Journal of Sociology, 96(6) 1991, p. 1464–77 [JSTOR]
2. Cantwell, G., Kirkley, A., and Newman, M., The friendship paradox in real and model networks. [arXiv]
3. Ugander, J., Karrer, B., Backstrom, L, and Marlow, C., The Anatomy of the Facebook Social Graph. [arXiv]

Historical probability of picking a perfect NCAA bracket 1985-2023

There is a lot of discussion of increasing parity in NCAA men’s basketball. For example, this year’s tournament saw another #16 seed upset a #1 seed in the first round, for only the second time in the history of the current 64-team tournament format going back to 1985. (As usual, I’m ignoring the nonsense of the four play-in games.) … But the first such first-round upset of a #1 seed was just 5 years ago in 2018.

Every year there is also discussion of the probability of picking a “perfect” tournament bracket– that is, what is the probability of correctly guessing the winners of all 63 games, from the first round to the championship? Estimating this probability is a convenient way to aggregate and weight the numerous upsets that happen each year (about 17.8 games on average) into a single number, that we can then use to compare the overall prior (un)likelihood of tournament outcomes across years.

All of the tournament history is available on GitHub, and this past article describes the details of methodology for modeling probabilities of individual game outcomes as a function of seed matchup. Here are the results updated to include this year’s tournament:

Probability of a perfect bracket, 1985-2023.

The constant black line at the bottom reflects the 1 in , or 1 in 9.2 quintillion exact probability of guessing any year’s outcome correctly, if you simply flip a fair coin to determine the winner of each game. The constant blue and red lines at the top indicate the estimated probability of a “chalk” bracket outcome, always picking the higher seeded team to win each match-up. (The blue and red colors reflect two different models of game probabilities as a function of difference in “strength” of each team; as discussed in the linked article, blue indicates a strength following a normal distribution density, and red indicates a simpler linear strength function.)

This year’s 2023 tournament made things particularly interesting, since we are now significantly “recalibrating” the single-game probability model (as a function of seed matchup) to nearly double the estimated probability of the most extreme 16-over-1 upset… and using that updated model to re-evaluate all past years.

In other words, despite deciding that a #16 upsetting a #1 seed is now, and has always been, twice as likely as we thought a year ago, this year’s tournament was still the most unlikely overall outcome ever– at least by the normal strength model (and the second-most unlikely by the linear strength model).

The hardest polycube packing puzzle

Introduction

I was recently playing with the Soma cube, a puzzle comprising a set of seven polycubes that can be assembled into a 3x3x3 cube, as shown below.

The Soma cube, disassembled into its seven polycubes (top), and one of its many solutions assembled into a 3x3x3 cube (bottom). Each polycube is labeled with its STL filename.

The Soma cube is one of the more widely known such “packing puzzles,” and although I’m not very good at solving puzzles like this– my wife is much better at this than I am– I didn’t find it terribly difficult to put together. This is maybe not very surprising: there are 11,520 possible oriented solutions, 480 distinct up to rotation of the cube. Which raised the question: how much harder can we make this puzzle? More precisely, among all puzzles of distinct polycubes to be packed into a 3x3x3 cube, is there a “hardest” such puzzle in some quantifiable sense, that agrees with our subjective human perception of difficulty?

Making polycubes

The first step toward answering this question was to make polycube puzzle pieces. Each polycube is a 3D-printed STL model, created using OpenSCAD and the PuzzleCAD library, that together made it very easy to generate nice models, including insetting faces and beveling edges of the cubies, so that puzzle pieces fit together easily but snugly. The following example script shows the PuzzleCAD parameters that I used (units are millimeters, so that a solved 3x3x3 cube is about 2 inches on each side), with the last line specifying the particular polycube to generate, in this example the tetracube 4-007 (shown above in magenta):

include <puzzlecad.scad>
$burr_scale = 17;
$burr_inset = 0.3;
$burr_bevel = 1.3;
$unit_beveled = true;
burr_piece(["xx|.x", "x.|.."]);

To generate the corresponding STL model file 4-007.stl in binary format, from the OpenSCAD input script file polycube.scad above:

openscad --export-format binstl -o 4-007.stl polycube.scad

All of the source code is available on GitHub, along with STL model files for all 207 polycubes up to hexacubes.

Measuring puzzle difficulty

We can enumerate all possible puzzles involving hexacubes or smaller as solutions to an exact cover problem, considering all possible positions and orientations of each polycube, searching for subsets of such oriented polycubes that exactly “cover” a 3x3x3 cube. However, each puzzle, defined as a subset of distinct unoriented polycubes (think of buying the puzzle pieces jumbled haphazardly in a bag), will generally appear some number times in this list of exact cover solutions, once for each way of positioning and orienting all of its particular polycubes. For example, even those puzzles with a unique solution will appear times, once for each possible rotation of the solved cube. The Soma cube appears times, with 24 “copies” of the 480 solutions that we would typically consider truly distinct, differing by more than just a rotation of the solved cube.

Intuitively, the larger the value of — the larger the number of oriented solutions– for a given puzzle, the “easier” it should be to solve. For example, the figure below shows one of the two puzzles maximizing , with 3,030,672/24=126,278 distinct solutions up to rotation. (The other “easiest” puzzle is essentially a “mirrored” version of this one, with polycube 4-007 replaced by its chiral counterpart 4-008.)

A candidate “easiest” puzzle, with the maximum number of oriented solutions.

So far, this tracks pretty well with manual experiment: no matter how you jumble these eight polycubes to start, they seem to almost “fall together” snowball-style into a solved 3x3x3 cube.

However, if we want the hardest puzzle, we want smaller values of , i.e., fewer solutions. But this metric alone still needs further refinement, since it turns out that, among all 19,276,753 possible puzzles involving hexacubes or smaller, 5,633,564 of them have unique solutions. That is, nearly 30% of all puzzles have the same minimum value . Surely some of these uniquely solvable puzzles are harder than others?

To handle this, I tried what seemed like the simplest thing that could possibly work: for each puzzle, define the difficulty “score” to be the ratio , where the numerator is the “breadth” of the brute force search tree. More precisely, counts how many ways we can (1) pick a first polycube, then (2) place and orient it somewhere in the yet-to-be-solved 3x3x3 cube. Put another way, is the number of rows in the matrix form of the “reduced” exact cover problem for that puzzle.

Intuitively, the larger the value of , the “wider” the search tree, and thus the harder it is to begin, so to speak, resulting in a larger difficulty score . Similarly, the smaller the value of , the fewer the number of possible solved configurations, also resulting in a larger difficulty score.

Results

The following histogram shows the resulting distribution of difficulty of all 19,276,753 possible puzzles involving hexacubes or smaller. Note that both axes are on a logarithmic scale; for example, the light and dark blue comprises the 387,347 puzzles without hexacubes, which make up only about 2% of the total.

Histogram of difficulties of all 19,276,753 puzzles involving hexacubes or smaller.

The two mirror-image easy puzzles described earlier live at the far left of this figure. At the far right of the figure, the two hardest puzzles, both with unique solutions, are also a chiral pair, one of which is shown below. (The other replaces polycube 6-057 with its mirror 6-095.)

The candidate hardest puzzle, maximizing the difficulty ratio r/s=33.

If we restrict our space of possible puzzles to pentacubes or smaller (shown in blue in the histogram above), then the hardest puzzle– again one of a chiral pair (the other replaces 5-024 with 5-027)– is shown below.

The candidate hardest puzzle maximizing the difficulty ratio r/s=32 subject to excluding hexacubes, i.e., with only pentacubes or smaller.

My wife was a helpful willing subject in these experiments. As mentioned, the easy puzzle was not even a puzzle, fitting together in seconds. The Soma cube was also straightforward, solved within minutes. To my delight, the two hardest puzzles above really were hard: it took a couple of hours to solve the pentacube version.

Interestingly, the hexacube version– with the slightly greater difficulty score– took less time, only about an hour. She did solve that one after the pentacube version, though; maybe we “warm up” our minds into puzzle-solving mode?

One way in which this difficulty metric seems flawed is that polycubes can contribute to a large tree breadth in two different ways: the single cubie, for example, can be positioned in 27 different locations in the 3x3x3 cube, despite lacking any distinct rotations; at the other extreme, even large polycubes, like most of the hexacubes, can be rotated into 24 different orientations, even if they don’t have much translational wiggle room. It’s not clear to me whether these two extremes should have similar contributions to difficulty score. (The polycube 5-026 above is an interesting middle ground, in that it’s asymmetric enough to have many orientations, but small enough to have many translations as well, so that it has the maximum overall contribution to tree breadth, with 192 possible oriented positions in the solved cube.)

A wrong solution to the Riddler sock matching problem

From last week’s FiveThirtyEight.com Riddler column:

From Anna Kómár comes a stumper about socks: In my laundry basket, I have 14 pairs of socks that I need to pair up. To do this, I use a chair that can fit nine socks, at most. I randomly draw one clean sock at a time from the basket. If its matching counterpart is not already on the chair, then I place it in one of the nine spots. But if its counterpart is already on the chair, then I remove it from the chair (making that spot once again unoccupied) and place the folded pair in my drawer. What is the probability I can fold all 14 pairs without ever running out of room on my chair?

This week’s column describes several solution approaches, including Monte Carlo simulation and recurrence relations. But here is another candidate approach that is potentially more efficient to compute:

Associate each possible sequence of sock drawings with a north-east lattice path, from when the basket is full, to when the basket is empty, with a north step corresponding to drawing an unmatched sock and placing it on the chair, and an east step corresponding to drawing a sock whose counterpart is already on the chair, removing, folding, and placing the pair in the drawer.

Valid drawing sequences are represented by such a lattice path that never touches the diagonal . (That is, we can’t have a negative number of socks on the chair.) There are of these paths (more on this later); of these, the number of successful drawing sequences, never running out of room on the chair, by also never touching the diagonal , is

Thus, the desired probability is 2660139/2674440, or about 0.994653.

This is effectively the argument made in Gilliand [1] and Pantic [2]. However, as pointed out by Paulsen [3], this incorrectly assumes that each distinct lattice path is equally likely, when in fact we are more likely to encounter paths requiring more room on the chair.

For this argument to work, we need a different problem: instead of 14 distinct (colors of) pairs of socks, suppose that we are folding 14 pairs of white athletic socks, essentially identical except for an “L” stitched on each left sock and “R” stitched on each right sock. Now, any left sock may be matched with any right sock and vice versa.

In this modified problem, valid drawing sequences are now all possible north-east lattice paths, and successful drawing sequences are paths strictly between the diagonals and . (That is, multiple socks on the chair must be all left or all right.) This does work, since each equally likely drawing sequence corresponds to a distinct lattice path. (The Riddler column does note that modeling the original problem using lattice paths is “tricky, since the probabilities of transitioning from one state to the next depended on how many paired and unpaired socks remained in the basket.” This is true… but that’s not really why the lattice path calculation doesn’t work in that case– even in this modified problem, state transition probabilities also depend on the composition of socks remaining in the basket.)

This version of the problem was discussed previously here; the motivation for this post is really just to collect my notes on the general solution to these counting problems (incorrectly applied in the former, correctly in the latter).

Theoerem: Given positive integers such that , the number of north-east lattice paths from to that do not intersect the diagonals nor is

Proof: First, reviewing the standard ballot-counting reflection argument: given a path to that does first intersect diagonal at , reflect the remainder of this path about that diagonal, so that the endpoint is reflected to . This establishes a bijection between the complementary set of diagonal-intersecting paths to and the set of all paths to .

We use this same technique here, but with repeated reflections: starting with all (unconstrained) paths to , we subtract those invalid paths that first intersect diagonal … but we must add back paths that subsequently also intersect diagonal , via a second reflection, etc. Similarly, we must also subtract invalid paths that first intersect diagonal , then add back paths that subsequently intersect diagonal , etc.

Grouping inclusion-exclusion terms by the number of initial diagonal intersections yields

the terms of which may be rearranged to yield the difference of sums above.

References:

1. Gilliand, S., Johnson, C., Rush, S., and Wood, D., The sock matching problem, Involve, 7(5) 2014, p. 691-697. [PDF]
2. Pantic, B. and Bodroza-Pantic, O., A brief overview of the sock matching problem. [arXiv]
3. Paulsen, W., The sock problem revisited, The College Mathematics Journal, 52(3) 2021, p. 193-203. [CMJ]

Probabilities in one-card Nomination Whist

My niece and nephew introduced me to a card game that they called Tricks, also known as Nomination Whist or Oh Hell. It’s a fun and interesting game, with simple rules but also with the potential for complex strategy. This post focuses on just one round in the game, played as follows:

Each of players is dealt card from a standard 52-card deck. One additional trump card is dealt face-up indicating the trump suit. Each player in turn starting left of the dealer plays the card from their hand, and the “trick” is won by either the highest-ranked card (ace is high) in the trump suit, or if no trump is played, by the highest-ranked card in the led suit. (In other rounds where , the player that wins the trick leads the next hand, continuing for a total of tricks in the round; players must follow the led suit if able.)

Between the deal and the play of the hand, each player in turn bids one or zero points (more generally up to points), indicating whether they think they will win the trick or not. The game is particularly interesting in that the objective is to win exactly the number of tricks bid, no more and no less.

Since you have no choices in how to play a hand with just one card, only bidding presents an opportunity for strategy. (Things are more complicated in rounds with more cards in the hand, hence the focus on the one-card case here.) How you should bid depends on the probability of winning the trick, which is in turn determined by one of four possible cases:

• Trump high: your card is in the trump suit, and ranks higher than the trump card.
• Trump low: your card is in the trump suit, and ranks lower than the trump card.
• Off suit lead: your card is off suit and leads, i.e., you are the player left of the dealer.
• Off suit follow: your card is off suit and follows, i.e., you are not the player left of the dealer.

The following table and figure show the formulas and probabilities, respectively, in each of these cases, as a function of your card’s rank (2=deuce through 14=ace) and the number of players.

Your card	Probability of winning
Trump high
Trump low
Off suit lead
Off suit follow

If everyone bids simultaneously, then this is essentially the whole story: bid one point if and only if the probability of winning indicated above is greater than 1/2. For example, in a four-player game, you should never bid for the trick with an off suit card, and always bid with trump… except with a deuce, or with a three where the deuce is the trump card.

But this oversimplifies the problem, since everyone does not bid simultaneously. Earlier players’ bids may inform and affect later players’ bids. The strategy complexity blows up quickly– analyzing even the simplest two-player game presents an interesting challenge: is optimal strategy a random mix of bluffing and/or slow play?

Counting marked dice

The following is from FiveThirtyEight.com’s Riddler:

I have an unlabeled, six-sided die. I make a single mark on the middle of each face that is parallel to one pair of that face’s four edges [see example in the figure below]. How many unique ways are there for me to mark the die? (Note: If two ways can be rotated so that they appear the same, then they are considered to be the same marking.)

Example marking of a die.

I think this is a particularly nice potential exercise for students for the usual reasons: on the one hand, wearing our mathematician hat, we can apply the lemma that is not Burnside’s… but this problem makes us think a bit harder about the coloring (i.e., how does each particular “color” represent an oriented mark on the die?), and about the distinction between the group of symmetries acting on the faces of the die versus the colorings of the faces of the die.

Alternatively, wearing our programmer hat, we can solve the problem (or maybe just verify our cocktail napkin approach above) by brute force enumeration of all possible markings, and count orbits under rotation with the standard trick of imposing some easy-to-implement ordering on the markings (converting each to its minimal representation under all possible rotations)… but again, what data structure should we use to represent a marking, that makes it easy to both enumerate all possibilities, and to compute orbits under rotation?

Following is my solution: we count the number of possible markings (“colorings”) that are fixed by each of the 24 rotational symmetries of the die, and average the results. To clarify the description of rotations, let’s temporarily distinguish one “red” face of the die, and group rotations according to the final location of the red face:

• If the red face stays in its original location, then:
  • The identity leaves all markings fixed.
  • Either of two quarter turns about the (axis normal to the) red face leaves zero markings fixed (since it changes the marking on the red face itself).
  • A half turn about the red face leaves markings fixed.
• If we rotate the red face a quarter turn to one of the four adjacent locations, then:
  • No additional rotation leaves zero markings fixed.
  • Either of two additional quarter turns about the (new axis normal to the) red face leaves markings fixed.
  • An additional half turn about the new red face leaves markings fixed.
• Finally, if we rotate the red face a half turn to the opposite face, then:
  • No additional rotation leaves markings fixed.
  • Either of two additional quarter turns about the new red face leaves markings fixed.
  • An additional half turn about the new red face leaves markings fixed.

Putting it all together, the number of distinguishable ways to mark the die is

All eight distinct ways to mark the die. Marks on opposing faces are the same color, with blue indicating parallel opposing marks, and red indicating skew (“perpendicular”) opposing marks.

The figure above shows the eight distinct ways to mark the die. Rather than “unfolding” the dice to explicitly show all six faces of each, the marks are colored red or blue, so that marks on opposing faces– one visible, one hidden– are the same color, with blue indicating parallel opposing marks, and red indicating skew, or “perpendicular,” opposing marks.

Analysis of horse racing board game

Introduction

I recently encountered a “horse racing” game played with two dice and a game board similar to the one shown in the figure below. Horses numbered 2 through 12 begin in the starting gate at the left, indicated by the green dots. At each turn, both dice are rolled yielding a total from 2 to 12, and the corresponding horse advances to the right one step, to the next black dot in their lane. The winner is the first horse to reach the finish line, indicated by the yellow dots.

Horse racing board game with the typical board layout.

What I found interesting about this game is the apparent intent to make the race fair. That is, for example, horse 7 is the most likely to advance on any particular dice roll, but this advantage is offset by requiring more steps to win. Indeed, if we describe the design of the board as a vector of integers indicating the required number of steps for each horse, in this case (3,6,8,11,14,17,14,11,8,6,3), then it makes at least some intuitive sense that these values are roughly in proportion to the corresponding dice probabilities.

However, this approach to leveling the playing field ends up being an extreme over-correction: horse 7 has way too far to go, winning the race less than 3% of the time, while Snake Eyes and Box Cars will each win over 19% of the time.

So, how can we fix this? Is there a better board design that more closely approximates a uniform distribution of wins across the eleven horses?

Scratching horses

First, I cheated a bit in the above description of the game. All eleven horses don’t actually race together; instead, before the race begins, the rules specify a procedure for scratching— i.e., removing from the race– four of the horses, and only the remaining seven horses race as described above. The scratching procedure is pretty simple: roll both dice, and scratch the corresponding horse. Continue rolling, ignoring rolls for horses that have already been scratched, until four distinct horses have been scratched. Similarly, during the race of the remaining seven horses, simply ignore any rolls for scratched horses. (I’m also leaving out the gambling nature of the game, which involves contributing chips or money to a winner-take-all pot with almost every dice roll; this scratching business really just serves to further increase the pot by stretching out the game a bit.)

To account for this, we need to compute the probability of scratching each of the C(11,4)=330 possible subsets of four horses, which we can then use to weight the probabilities of each of the unscratched horses subsequently winning the race.

Given a particular subset of four horses, we compute the probability of exactly that subset being scratched by solving for in the linear system of equations in variables, indexed by subsets of , where

where is the single-roll probability of advancing horse (e.g., , etc.). In Python with SymPy (all code is available on GitHub):

def p_scratch(q):
    """Probability of scratching subset with dice probabilities q[:]."""
    a = sympy.eye(2 ** len(q))
    for i in range(2 ** len(q) - 1):
        for h, p_roll in enumerate(q):
            j = i | (2 ** h)
            a[i, j] -= p_roll
    return sympy.linsolve((a, sympy.eye(2 ** len(q))[:, -1])).args[0][0]

Win probabilities

At this point, given a particular subset of seven unscratched horses in a race, we are prepared to compute the probabilities of each of those horses winning, with a relatively simple modification of the generating function approach described in this earlier post, as the sum of coefficients for horse , where

and is the number of steps required for horse to win. Again in Python with NumPy (and the fractions module in case we want exact results):

def p_win1(p, n):
    """Probability of first horse winning."""
    g1 = P.polypow([Fraction(0), p[0]], n[0] - 1) / np.math.factorial(n[0] - 1)
    g2 = reduce(P.polymul,
                ([pi ** k / np.math.factorial(k) for k in range(ni)]
                 for pi, ni in zip(p[1:], n[1:])))
    g = reduce(P.polymul, [[p[0]], g1, g2])
    return sum(c * np.math.factorial(m) for m, c in enumerate(g))

Putting it all together, computing the overall probabilities of each horse winning the race after scratching four of the horses, it turns out that the scratching just makes the non-uniformity even worse, although only slightly: horse 7 now wins less than 2.5% of the time, and horses 2 and 12 win over 20% of the time.

Evaluating all board designs

So, finally, we can turn the above crank on each of the C(17+6-1,6)=74,613 different possible “reasonable” board designs, where by “reasonable” I mean symmetric (horses like 2 and 12 with the same dice probability should require the same number of steps to win) and monotonic (a horse like 7 with higher dice probability should never require fewer steps to win), ranging from the simplest first-roll-wins board (1,1,1,1,1,1,1,1,1,1,1) to the longest-race-but-still-unfair board (17,17,17,17,17,17,17,17,17,17,17). The figures below show some of the best results.

Probabilities of each horse 2-12 winning a race on various board designs (see colors below): at left, scratching no horses so that all 11 horses race; at right, scratching 4 horses and racing the remaining 7.

As already discussed, the original game board (3,6,8,11,14,17,14,11,8,6,3) fares pretty poorly. Interestingly, if we ignore scratching and just race all eleven horses together (figure at left), then the fairest board is pretty unambiguously (2,3,4,5,6,7,6,5,4,3,2)— almost but not quite the same as this Canadian version of the game– which minimizes all three of the norm (proportional to total variation distance), the norm, and the relative entropy distances from the uniform distribution.

If we play the standard game with four scratched horses (figure at right), then there are a few options depending on the yardstick for fairness. The board (4,7,9,11,13,15,13,11,9,7,4) minimizes the norm, and comes in third for the other two measures. The board (4,6,8,10,12,13,12,10,8,6,4) minimizes the norm and relative entropy, and comes in second for the norm. Alternatively, the board (4,6,8,10,12,14,12,10,8,6,4) comes in second, for both the no-scratch and four-scratch variants of the game, and for all three measures… except for the four-scratch norm, where it comes in fifth out of all candidate boards.

Rube Goldberg Monte Carlo

Introduction

“This shouldn’t take long,” Alice says. “It’s only flipping a coin, after all.”

Alice and Bob are talking in the hallway at work. Alice has been tasked with analyzing the behavior of a simple black box. When a button on the side of the box is pressed, a mechanism inside the box flips a biased coin, and displays either a green light when the coin comes up heads– with some fixed but unknown probability — or a red light when it comes up tails.

“As we discussed in the meeting, I will press the button to flip the coin 200 times, observe the number of green and red light indications, and report the resulting 95% confidence interval bounds for — to two digits, as usual*.”

“That’s great for you,” Bob grumbles. “I’m the one stuck with analyzing the Rube Goldberg Variation.”

Bob’s task is more involved. The Rube Goldberg Variation is a much larger black box, taking up almost an entire room. Instead of just a button on the outside of the box, there is a dial as well, that may be set to a positive integer specifying the “mode” in which the box is configured.

The mechanism inside is much more complex as well: pressing the button on the side of the box starts a convoluted sequence of interacting mechanisms inside, many of which exhibit some randomness similar to Alice’s coin flip. This process takes several minutes… but eventually, the box displays either a green light indicating “success” — with some fixed but unknown probability 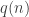that depends on the selected mode– or a red light indicating “failure.”

“I suppose the good news is that at least we’re only focusing on the one mode 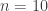,” Bob says. “But this analysis is still going to take days to complete. Not only does each single experiment– from pressing the button to observing the light– take longer, but I will also need more sample outcomes of the experiment to estimate 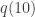with the same degree of certainty.”

Alice looks confused. “Wait, why do you need more samples? Shouldn’t the usual 200 be enough?”

Bob replies, “If it were just a coin flip, sure. But the Rube Goldberg Variation has a lot more moving parts, with a lot more opportunities to introduce randomness into the process. I need more samples to cover all of the possible combinations of corner-case interactions between all of those components.”

Monte Carlo simulation

This post is motivated by Bob. Recently, Bob was an undergraduate student… but I’ve also encountered discussions like the one above when Bob has been a computer scientist with a Ph.D. So, this is my attempt to capture my thoughts on this subject, to hopefully highlight the specific areas where there are potential pitfalls and opportunities for confusion.

In these past discussions, there were not any actual black boxes. Instead, there were computer simulations of the processes inside hypothetical black boxes. For example, the simulation of Alice’s black box might look like this (in Python):

def alice():
    return 1 if random.random() < 0.75 else 0

where we can estimate the probability of success by evaluating alice() many times and averaging the results. Of course, that would be a bit ridiculous if we were allowed to inspect the source code, since we could just read directly that .

But now consider Bob’s more complicated simulation:

def bob(n):
    position = 1
    while True:
        while True:
            move = random.randint(-1, 1)
            if 1 <= position + move <= n:
                break
        position = position + move
        if move == 0:
            break
    return 1 if position == 1 else 0

(In reality, Bob’s simulation should be much more complicated than this, with so many lines of code, and so many random components, that analysis by inspection is practically impossible. But I can’t resist inserting a tractable puzzle even when it’s not the point: inside this black box, there are 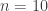slots arranged in a row, with a marble initially in the left-most slot. When Bob presses the button, the marble makes a series of random moves, with each move selected uniformly from {left, stop, right}. An attempt to move left beyond the left-most slot, or right beyond the right-most slot, is ignored. The marble moves randomly back and forth along the row of slots, until a “stop” move, resulting in display of a “successful” green light if the marble stops in its original left-most slot, or a “failure” red light otherwise.)

It’s at least not as immediately clear from inspection alone what is the probability 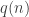that bob(n) returns 1… indeed, with those nested while True loops in there, it might not be obvious whether this function is guaranteed to return at all (fortunately, it is– more on this later).

So, to level the playing field, so to speak, let’s suppose that neither Alice nor Bob is able to inspect their simulation source code at all. In other words, neither is allowed to open their black box and peek inside; all either can do is inspect their black box’s output, observed from repeatedly pressing the button on the side of the box. (Remember, Bob was the one complaining; so we’re trying to remove any unfair advantage that Alice might have.)

Given this setup, we are considering the following question: because Bob’s simulation is more complex, does he require more sample executions of his simulation to estimate 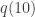, than Alice requires to estimate with the same degree of certainty?

A simulation is a function

I think it’s helpful to think of a simulation like those above as a function, in the mathematical sense; that is, a simulation is a function

that maps its input to a binary output 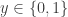, that is,

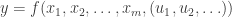
where the output 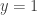means “success” and 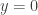means “failure.”

The input parameters specify the configurable “mode” of the simulation. In Alice’s case, 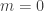since her simulation isn’t configurable. In Bob’s case, 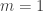and , where he is interested in the specific case .

The inputs 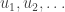specify a single realized sample of a pseudo-random number stream, where each 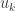is drawn independently and uniformly from the unit half-open interval . This is enough expressive power to represent effects of the random processes in any computable simulation: in the context of the Python implementations above, each 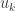is the result of the k-th evaluation of random.random(), which we can think of as the “subroutine” in terms of which all other pseudo-random functions, like random.randint(a, b), or random.gauss(mu, sigma), etc., may be implemented.

(Pseudo) randomness

I think viewing the “random” behavior of a computer simulation in this mathematical way is useful, since it forces us to consider some important implementation details. Note that by specifying our simulation as a function, we require that the function be well-defined. That is, every possible input must map to a unique output.

Input must map to a unique output: in other words, our simulation must be repeatable. Given the same input values– specifying both the configuration parameters as well as the sampled random number stream 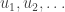— the simulation must always return the same output value, either always 0 or always 1. Output cannot vary depending on “hidden” additional factors outside the domain of the function, such as the system clock’s indication of the current time, etc.

Every input must map to an output: here we need to be careful about guaranteeing that our simulation will terminate. That is, in any particular practical execution of the simulations above, we never need the entire sequence of “available” random numbers (since otherwise it would run forever). For example, Alice’s simulation only ever depends on the first random draw . Bob’s simulation, on the other hand, depends on an unbounded but finite number of draws that varies from one run to the next. That is, there is a positive probability that running the simulation could take an hour, or a week, or a year, or any specified amount of time, no matter how long… but there is zero probability that it will run forever.

But there are input sequences in the domain of the simulation function that correspond to this “run forever” behavior. For example, in Bob’s simulation, what if the marble selects the “left” move at every turn? Or alternates “left” and “right,” without ever selecting “stop”? For our function to be well-defined, we still need to assign some output to any and all of these infinite-length inputs in the domain, even if they have zero probability of occurring.

The good news is that we can assign any output we want… because it doesn’t matter! That is, no matter what questions we might ask about the statistical behavior of the output of a (terminating) simulation, the answers do not depend on our choice of assignment of outputs to those “impossible” outcomes.

More precisely, we can change our perspective slightly, and view our simulation function as a random variable on the sample space with its natural probability measure, parameterized by the simulation mode:

where we don’t care about the output from those “impossible” outcomes because they have measure zero. Note that this is essentially just a notational change, not a conceptual one: a random variable is neither random, nor a variable; it’s simply a function, just like we started with. This random variable has a Bernoulli distribution, whose parameter 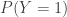we are trying to estimate… which we can do, no matter the “complexity” of the simulation realizing the function .

Conclusion

So, the answer to the question posed here– does Bob need more random samples than Alice to do his job– is no. The black boxes are black; we can’t peek inside them. They are effectively indistinguishable by anything other than their behavior. Similarly, a function implementing a simulation is characterized not by its “complexity” of “implementation,” but solely by its mapping of inputs to outputs.

I’m pretty sure I’ve already beaten this horse to death. But there are several other interesting wrinkles not discussed here. For example, we often want to actually no-kidding repeat exactly the same past simulation behavior (when debugging, for example); this capability is managed by using and recording seeds and/or substream indices as “shorthand” for the infinite sequences 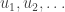of input random numbers. Also, the input configuration parameters have so far been mostly just additional notational noise. But that configurability can lead to additional analysis pitfalls, when combining Monte Carlo observations of simulation runs across different values of those configuration parameters.

Notes

(*) When reporting on results of the analysis, why the frequentist Clopper-Pearson confidence interval instead of a more fashionable Bayesian approach of reporting, say, the (narrowest) highest density credible interval with, say, a uniform prior? Since those decisions weren’t really the point here, I chose the experimental setup carefully, so that it doesn’t matter: the resulting intervals, reported to two digits of precision, will be the same either way. If there is any safe place to be a frequentist, it’s on a computing cluster.

NCAA tournaments are getting measurably wilder

Last night, the #1 seed Kansas Jayhawks won the NCAA men’s basketball tournament. Maybe an unsurprising outcome… but they defeated #8 seed North Carolina in the championship game. Only four #8 seeds have made it that far in the nearly four decades of the current format.

This year’s tournament also saw #15 seed Saint Peter’s advance to their regional final, the first #15 seed ever to do so.

And there were plenty of other unlikely upsets as well. Considering the tournament as a whole, that is, all 63 games (ignoring the abomination of the four play-in games) and their seeding match-ups, how “wild” was this year’s outcome compared to past tournaments?

Or, put another way, what was the prior probability of picking a “perfect bracket,” guessing every game outcome correctly, and how does that probability compare with past years?

This question has been discussed here before; I won’t rehash the details of this past article that describes the details of methodology for modeling game probabilities. This post is really just bringing that analysis up to date to reflect recent tournaments (all source historical tournament data is available on GitHub). Here are the results:

Probability of a perfect bracket, 1985-2022.

The constant black line at the bottom reflects the 1 in , or 1 in 9.2 quintillion probability of guessing any year’s outcome correctly, if you simply flip a fair coin to determine the winner of each game. The constant blue and red lines at the top are for comparison with the actual outcomes, indicating the probability of a “chalk” bracket outcome, always picking the higher seeded team to win each match-up. (The blue and red colors reflect two different models of game probabilities as a function of difference in “strength” of each team; as discussed in the previous article, blue indicates a strength following a normal distribution density, and red indicates a linear strength function.)

By either the normal or linear models, three of the last four tournaments (2018, 2021, and 2022– 2019 was pretty by the book, and 2020 was, well, 2020) were among the top five “wildest,” most unlikely outcomes in the last four decades.